Post Tuned Hashing - A New Approach to Indexing High-dimensional Data

论文阅读：Post Tuned Hashing: A New Approach to Indexing High-dimensional Data

1. 方法介绍

Learning to hash是进行高维数据索引的有效方法，它的目标是：学习一个low-dimensional的、similarity-preserving的二进制编码表示，使该其可以代表原高维空间的数据。本文基于Unsupervised hashing method思想，通过探索数据内在特征与属性，来学习二进制码表示。

传统的无监督hashing基本都通过2阶段的范式来实现：

1. mapping：将高维原始数据投影到低维空间；
2. binarization：将投影向量二值化，变成一个“二进制”编码。

并且为了保证原有的neighborhood relationships，他们大都选择在投影阶段或者二值化阶段做出优化。

但是，论文指出，尽管他们努力地在某个阶段保证了邻域关系(例如在降维时保证了邻域关系)，但是二值化过程不可避免地造成了neighborhood error：即原数据中相邻的数据可能会产生不相似的二进制编码，而不相邻数据可能会产生相似编码。于是论文提出了一个全新的步骤，post-tuning stage，意图使用该方法在二值化后重建邻域关系，减小邻域损失。图1展示了加入新的步骤前后，邻域损失情况。

图1. Toy illustration of the superiority of post-tuning.

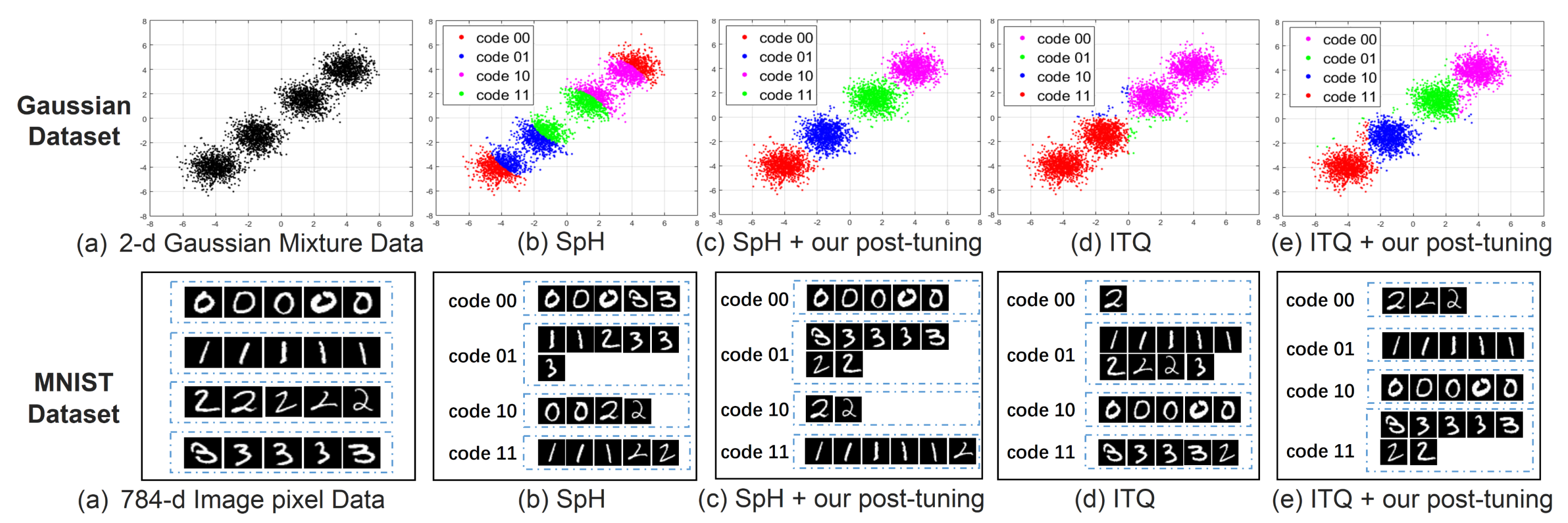
值得注意的是，该步骤独立于前两个步骤，因此可以广泛适配传统的2阶段方法。

2. 方法框架分析与推导

下面我们对该方法的理论做一定的阐述与推导：

首先，我们设数据集 $X\in \Bbb{R}^{d\times n}$ 包含n个数据，每个数据的维度为d。为了完成无监督hashing的两个阶段，我们可以通过一个线性或非线性的函数 $P:\Bbb{R}^d \rightarrow \Bbb{R}^m$完成高维到低维的投影，再通过一个二值化函数$sgn(\cdot)$ 将低维向量二值化：

$$Z = H(X) = sgn(P(X))\tag{1}$$

其中 $sgn:\Bbb{R}^m \rightarrow {-1, 1}^m$，其根据每个元素是否大于0进行二值划分。

由于论文指出上述2阶段方法会造成严重的neighborhood error，因此他们定义了该损失函数的表达式：

$$\mathcal{L} = \Vert S - V \Vert_F^2\tag{2}$$

其中 $S\in \Bbb{R}^{n\times n}$ 是原始数据的邻域关系矩阵，定义为

$$S_{ij} = \begin{cases} \begin{aligned} 1 \quad &\text{if}\ d(x_i, x_j) < \epsilon\\ -1\quad &\text{otherwise} \end{aligned} \end{cases}$$

$d(\cdot)$ 衡量了原始数据空间的欧氏距离。而 $V$ 是二值化空间的邻域关系矩阵，定义为

$$V_{ij} = \left( b_i\cdot b_j \right) / m \tag{3}$$

其中，b_i 是数据 x_i 的二值化向量。可以看到V_ij 是值域为-1到1的离散变量。那么通过式(3)，损失函数可以改写为：

$$\mathcal{L} = \Vert S - \frac{1}{m}B^TB \Vert_F^2\tag{4}$$

其中 $B\in {-1, 1}^{m\times n}$是n个数据的二值化向量矩阵。

结合公式(1)和公式(4)，很容易得到在传统方法中，$B = H(x)$。现在，作者希望通过加入第3个步骤，即Post Tuned Hashing (PTH)，来实现二值化向量的重建。具体而言，论文将定义一个新的变换 $R:{-1,1}^m\rightarrow {-1,1}^m$，使得重建后的二值向量能够最小化损失：

$$PTH(X) = R(H(X))\tag{5}$$

对于这个新的变换，论文设计了一个二值(-1,1)的矩阵post-tuning matrix，表示为 $U\in \Bbb{R}^{m\times n}$，通过学习这个矩阵来使损失最小化。这样，公式(4)可以进一步写为

$$\min \mathcal{Q}(U) = \Vert S - \gamma (U\circ Z)^T(U\circ Z) \Vert_F^2\tag{6}$$

为了清楚地推导论文的优化算法，这里对于步骤做了细化的分析：

$$\begin{aligned} U\circ Z &= \begin{bmatrix} {u_{11}}&{u_{12}}&{\cdots}&{u_{1n}}\\ {u_{21}}&{u_{22}}&{\cdots}&{u_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {u_{m1}}&{u_{m2}}&{\cdots}&{u_{mn}}\\ \end{bmatrix}\circ \begin{bmatrix} {z_{11}}&{z_{12}}&{\cdots}&{z_{1n}}\\ {z_{21}}&{z_{22}}&{\cdots}&{z_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {z_{m1}}&{z_{m2}}&{\cdots}&{z_{mn}}\\ \end{bmatrix}\\ &= \begin{bmatrix} {u_{11}z_{11}}&{u_{12}z_{12}}&{\cdots}&{u_{1n}z_{1n}}\\ {u_{21}z_{21}}&{u_{22}z_{22}}&{\cdots}&{u_{2n}z_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {u_{m1}z_{m1}}&{u_{m2}z_{m2}}&{\cdots}&{u_{mn}z_{mn}}\\ \end{bmatrix} \end{aligned}\tag{7}$$ $$\begin{aligned} &S - \gamma(U\circ Z)^T(U\circ Z)\\ &= S - \gamma \begin{bmatrix} {u_{11}z_{11}}&{u_{21}z_{21}}&{\cdots}&{u_{m1}z_{m1}}\\ {u_{12}z_{12}}&{u_{22}z_{22}}&{\cdots}&{u_{m2}z_{m2}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {u_{1n}z_{1n}}&{u_{2n}z_{2n}}&{\cdots}&{u_{mn}z_{mn}}\\ \end{bmatrix} \begin{bmatrix} {u_{11}z_{11}}&{u_{12}z_{12}}&{\cdots}&{u_{1n}z_{1n}}\\ {u_{21}z_{21}}&{u_{22}z_{22}}&{\cdots}&{u_{2n}z_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {u_{m1}z_{m1}}&{u_{m2}z_{m2}}&{\cdots}&{u_{mn}z_{mn}}\\ \end{bmatrix}\\ &= S - \gamma \begin{bmatrix} {\sum_{k=1}^mu_{k1}z_{k1}u_{k1}z_{k1}}&{\sum_{k=1}^mu_{k1}z_{k1}u_{k2}z_{k2}}&{\cdots}&{\sum_{k=1}^mu_{k1}z_{k1}u_{kn}z_{kn}}\\ {\sum_{k=1}^mu_{k2}z_{k2}u_{k1}z_{k1}}&{\sum_{k=1}^mu_{k2}z_{k2}u_{k2}z_{k2}}&{\cdots}&{\sum_{k=1}^mu_{k2}z_{k2}u_{kn}z_{kn}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {\sum_{k=1}^mu_{kn}z_{kn}u_{k1}z_{k1}}&{\sum_{k=1}^mu_{kn}z_{kn}u_{k2}z_{k2}}&{\cdots}&{\sum_{k=1}^mu_{kn}z_{kn}u_{kn}z_{kn}}\\ \end{bmatrix} \end{aligned}\tag{8}$$ $$\Rightarrow \left[(U\circ Z)^T(U\circ Z) \right]_{ij} = \sum_{k=1}^mu_{ki}z_{ki}u_{kj}z_{kj}\tag{9}$$

根据上面的详细推导，我们的目标函数可以写为

$$\begin{aligned} &\min \mathcal{Q}(U) = \Vert S - \gamma (U\circ Z)^T(U\circ Z) \Vert_F^2\\ \Leftrightarrow &\min_{U} \sum_{ij}\left[ S_{ij} - \gamma\sum_{k=1}^mu_{ki}z_{ki}u_{kj}z_{kj} \right]^2 \end{aligned}\tag{10}$$

我们也可以统计U的第p行的部分：

$$\begin{aligned} &\sum_{ij}\left[ S_{ij} - \gamma\sum_{k=1}^mu_{ki}z_{ki}u_{kj}z_{kj} \right]^2\\ =&\sum_{ij}\left[ S_{ij} - \gamma\left( u_{pi}z_{pi}u_{pj}z_{pj} + \sum_{k=1,k\neq p}^mu_{ki}z_{ki}u_{kj}z_{kj} \right) \right]^2\\ \mathop{=}\limits_{x=u_{pi}z_{pi}u_{pj}z_{pj}}^{\mathrm{set}\ A=\sum_{k=1,k\neq p}^mu_{ki}z_{ki}u_{kj}z_{kj}}& \sum_{ij}\left[ S_{ij} - \gamma\left( x + A \right) \right]^2\\ =& \sum_{ij}S_{ij}^2 - 2\gamma S_{ij}(x+A) + \gamma^2(x+A)^2\\ \mathop{=}\limits^{\mathrm{delete}\ \mathrm{without}\ x}& \sum_{ij} -2\gamma S_{ij}x + \gamma^2x^2 + 2\gamma^2A\cdot x \end{aligned}\tag{11}$$

所以一次项，即文章中的linear terms，可以表示为

$$\begin{aligned} &\sum_{ij}-2\gamma S_{ij}x+2\gamma^2A\cdot x\\ =& -2 \sum_{ij}u_{pi}z_{pi}u_{pj}z_{pj}\left[ \gamma S_{ij} - \gamma^2\left( \sum_{k=1,k\neq p}^mu_{ki}z_{ki}u_{kj}z_{kj} \right) \right] \end{aligned}\tag{12}$$

论文设 $Z$ 的第p行的数据为 $z$_p，其转置(即column向量)为 $\overline{z}$_p，设 $Q=\overline{z}_p \overline{z}_p^T$ ， 设 $(U \circ Z)_{\backslash p}$ 是将公式(1)的第p行删除的新矩阵，设 $O = \left[(U \circ Z)_{\backslash p} \right]^T\left[(U \circ Z)_{\backslash p}\right]$ ，我们可以轻易地将公式(5)改写为

$$-2\gamma\sum_{ij}u_{pi} Q_{ij}\left(S_{ij} - \gamma O_{ij} \right) u_{pj}\tag{13}$$

值得指出，$Q_{ij} = z_{pi}z_{pj} = Q_{ji}, \quad O_{ij} = \sum_{k=1,k\neq p}^mu_{ki}z_{ki}u_{kj}z_{kj} = O_{ji},\quad S_{ij} = S_{ji}$ (详见论文公式(4))，那么如果我们设 $ C = Q\circ (S - \gamma O) $ ，那么 $C$ 就是对称矩阵。因此公式6可以进一步化简：

$$-2\gamma\sum_{ij}u_{pi}c_{ij}u_{pj}\tag{14}$$

其中，每一个涉及$u_{pq}$的量均可以表示为：

$$\begin{aligned} -2\gamma\sum_{i=q,j}u_{pq}c_{qj}u_{pj} - 2\gamma\sum_{i,j=q}u_{pi}c_{iq}u_{pq} &= - 4\gamma\sum_{k}u_{pk}c_{qk}u_{pq}\\ &= -4\gamma\sum_{k=1,k\neq q}^nu_{pk}c_{qk}u_{pq} + 二次项 \end{aligned}\tag{15}$$

对于每一个元素 $u_{pq}$ ，最小化损失函数公式(6)即最小化公式(15)。我们可以将 $u_{pq}$ 前面的系数当成是权重，那么为了最小化损失，当权重为负时，我们希望 $u_{pq}=1$ ，权重为正时反之。

更新与优化策略

论文提供了一种更新策略：

update the current entry if its coefficient is larger than a fixed threshold $\eta$.

这个策略可以按照矩阵$U$内的元素顺序进行依次更新，减小了算法复杂度。并且，在一行元素更新时，矩阵 $C$并不需要更新，这是因为$C$受到 $U$所有元素的影响，对一行数据的改变不敏感。

论文提供了一种剪枝策略：

Only tune the elements whose projection results (value before binarization) are close to 0, or smaller than a threshold $\delta$.

即，我们只调整那些投影后值与0接近的元素(因为0是二值化的一个阈值)，因为这些元素更有可能被二值化为不正确的值。这有效减少了post-tuning的复杂度，并且缓解了过拟合。

结合这两种策略，最终的优化算法如下图所示：

图2. Post-tuning Algorithm

Out-of-Sample Post-Tuning

由于是无监督学习方法，故方法必须兼容新的数据 $q \notin X$。与K近邻的思想类似，新来的数据 $q$ 理应与原来的数据 $X$产生联系。因此，我们称原来的数据为skeleton points。这样，完整的post-tuning应该包含以下2个任务：

1. post-tuning skeleton points $X$；
2. post-tuning out-of-sample $q$.

与公式(6)类似的，我们建立如下损失：

$$\begin{aligned} \min \mathcal{R}(u^q) &= \Vert S^q - \frac{1}{m}(u^q\circ z^q)^T B \Vert_F^2\\ \text{s.t.} &\quad u^q\in \{-1,1 \}^m \end{aligned}\tag{16}$$

其中:

• $S^q\in \Bbb{R}^{1\times n}$：$q$ 和 $X$的邻域关系矩阵；
• $u^q\in \Bbb{R}^{1\times m}$：即 $q$ 的post-tuning matrix；
• $z^q\in \Bbb{R}^{1\times m}$：即 $q$ 经过二值化后的向量；
• $B = (U\circ Z) \in \Bbb{R}^{m\times n}$：$X$经过post-tuning的新二值化向量。

总之上式衡量了hashing前后 $q$ 和 $X$ 的邻域关系。论文也提到，由于post-tuning完全独立于前面2个步骤，因此这里的skeleton points( $X$ )在实践中并不是全部训练集，而是选择少部分数据点以提高效率。数据点数量的选择和最终方法效果的关系可从下图得出

图2. Post-tuning Algorithm

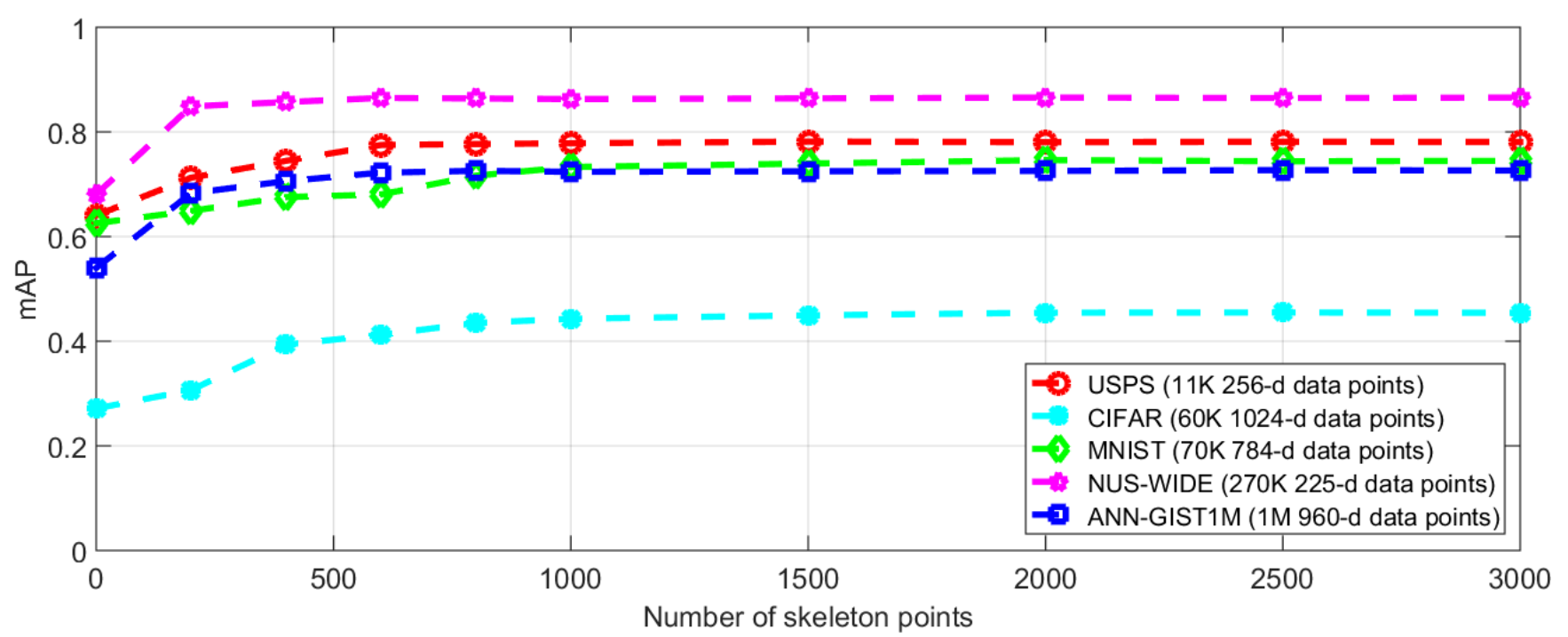
适量的数据点即可达到性能上限。太多的数据点不仅不能提高性能，还会消耗过多空间/时间资源。