Proximal Policy Optimization(PPO)

llama-v2昨日开源，看论文的过程中发现自己遗忘了PPO算法。赶紧回顾了Hongyi Li的视频，现在趁还有记忆推导一下。

Policy gradient推导

PPO算法的本质还是训练一个Policy model，来模拟actor根据当前状态进行决策的过程。接下来我们来推导求得训练的损失函数。

首先，切莫忘记强化学习有3个基本元素：Actor，Environment，Reward。假设我们现在正在玩一局游戏，那么当我们结束游戏蓦然回首，可以得到下面这张图：

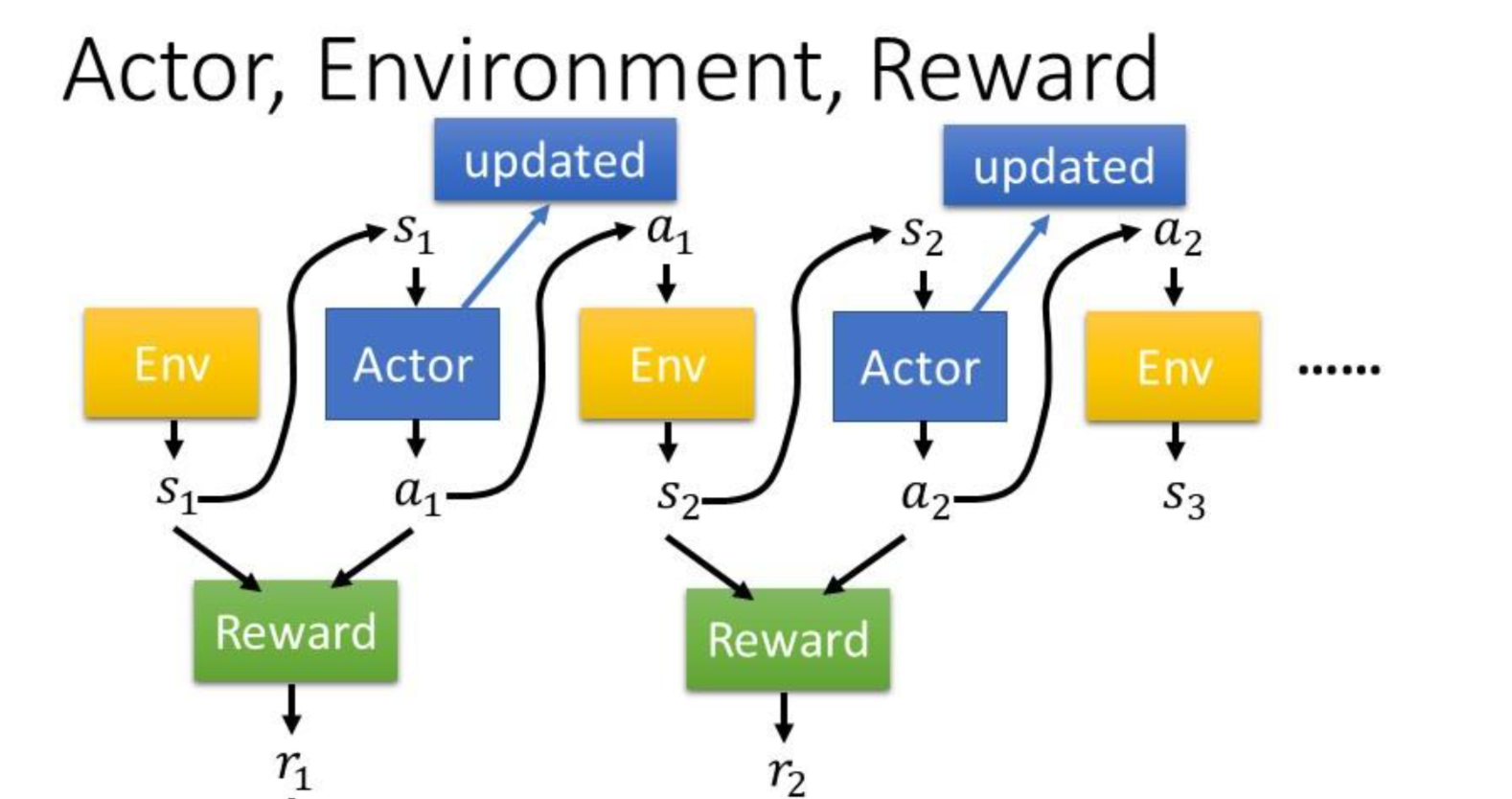
其中我们可以得到一个序列(Trajectory)：$\tau = {s_1,a_1,s_2,a_2,…,s_T,a_T }$，易知该序列记录了你在玩游戏时遇到的环境$s_i$及你采取的动作$a_i$。

现在，我们假设进行动作决策的Policy model是$\pi_{\theta}$，这是一个deep network。我们可以轻易算得这个序列出现的概率：

$$\begin{aligned} p_{\theta}(\tau) &= p(s_1)\cdot p_\theta(a_1|s_1)\cdot p(s_2|s_1,a_1)\cdot p(a_2|s_2)\cdot ... \cdot p(s_{T+1}|s_{T}, a_{T})\\ &= p(s_1) \prod_{t=1}^T p_{\theta}(a_t|s_t) \cdot p(s_{t+1}|s_t,a_t) \end{aligned}\tag{1}$$

可以看出，这个序列(这轮游戏)的概率，受环境(决定各个状态出现的概率)和policy model的影响。同时，我们记录这个序列的总体回报，即Reward：

$$R(\tau) = \sum_{t=1}^T r_t\tag{2}$$

其中$r$是采取每一个action后获得的回报，我们对其求和获得总回报。

现在，我们希望学习一个policy model，使其可以让平均回报，或者说回报的期望达到最大，这样对于任意的一局游戏，我们都会倾向于获得更多回报。即

$$\max \overline{R}_{\theta} = \int_{\tau} R(\tau) \cdot p_{\theta}(\tau) \ d\tau = \sum_{\tau}R(\tau) \cdot p_{\theta}(\tau)\tag{3}$$

现在，我们以上式作为目标函数，则其偏导(关于模型参数)为

$$\begin{aligned} \nabla \overline{R}_{\theta} &= \sum_{\tau} R(\tau) \cdot \nabla p_{\theta}(\tau)\\ &= \sum_{\tau} R(\tau)\cdot p_{\theta}(\tau) \nabla\log p_\theta(\tau) \\ &= \Bbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log p_\theta(\tau)] \approx \frac{1}{N}\sum_{n=1}^N R(\tau^n)\nabla\log p_\theta(\tau^n)\\ &= \frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}R(\tau^n)\nabla\log p_{\theta}(a_t^n|s_t^n) \end{aligned} \tag{4}$$

其中，我们可以采样N次序列(理解为N局游戏)来近似偏导的期望，并采用梯度更新来更新模型:
$\theta \leftarrow \theta + \eta \nabla \overline{R}\theta$
. 这里值得注意的是，更新了参数之后，policy model $\pi{\theta}$ 会发生变化，需重新采样而不能再使用原来的数据。

最后，如果考虑$R(\tau)$是权重，那么给这个序列的每一个状态-动作对$(s_i,a_i)$相同的权重是不合适的，因为并不是所有状态-动作对都与这个最终结果，即$R(\tau)$呈正相关。最终，我们假设每个状态动作对的权重只与从该状态-动作对开始的总reward为权重，并辅以一个时间衰减参数$\gamma<1$，得到最终的偏导：

$$\nabla \overline{R}_\theta \approx \frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}\left(\sum_{t'=t}^{T_n}\gamma^{t'-t}r_{t'}^n - b \right)\nabla\log p_{\theta}(a_t^n|s_t^n) = \frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}A^\theta(s_t,a_t)\nabla\log p_{\theta}(a_t^n|s_t^n)\tag{5}$$

off-policy

我们发现，由于我们不断的更新模型参数，导致数据只能使用一遍。但如果我们采用off-policy策略，即用于训练更新的模型和用于在环境中交互的模型不是同一个，那么数据就可以重复利用了。

那么我们现在只有关于交互模型$q$的采样数据，如何去估计需要训练的这个模型$p$的期望呢？我们引入Importance Sampling，即

$$\Bbb{E}_{x\sim p}[f(x)] = \int f(x)p(x)dx = \int f(x)\frac{p(x)}{q(x)} q(x)dx = \Bbb{E}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\tag{6}$$

应用到policy gradient，公式(5)可以改写为

$$\begin{aligned} \nabla \overline{R}_\theta &= \Bbb{E}_{(s_t,a_t)\sim \pi_\theta}\left[A^{\theta}(s_t,a_t)\nabla\log p_{\theta}(a_t|s_t) \right]\\ &= \Bbb{E}_{(s_t,a_t)\sim \pi_\theta'}\left[\frac{p_{\theta}(s_t,a_t)}{p_{\theta'}(s_t,a_t)}A^{\theta'}(s_t,a_t)\nabla\log p_{\theta}(a_t|s_t) \right]\\ &= \Bbb{E}_{(s_t,a_t)\sim \pi_\theta'}\left[\frac{p_{\theta}(a_t|s_t)p_{\theta}(s_t)}{p_{\theta'}(a_t|s_t)p_{\theta'}(s_t)}A^{\theta'}(s_t,a_t)\nabla\log p_{\theta}(a_t|s_t) \right],\quad \text{let}\ p_{\theta}(s_t)=p_{\theta'}(s_t) \\ &= \Bbb{E}_{(s_t,a_t)\sim \pi_\theta'}\left[\frac{p_{\theta}(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)\nabla\log p_{\theta}(a_t|s_t) \right], \quad \text{use}\ \nabla f(x) = f(x)\nabla \log f(x)\\ &= \Bbb{E}_{(s_t,a_t)\sim \pi_\theta'}\left[\frac{\nabla p_{\theta}(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)\right] \end{aligned}\tag{7}$$

那么我们的损失函数可设为

$$J^{\theta'}(\theta) = \Bbb{E}_{(s_t,a_t)\sim \pi_\theta'}\left[\frac{p_{\theta}(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)\right]\tag{8}$$

最后的最后，需要注意Importance Sampling中2个分布p和q差异不能太大(为什么？)，因此引入一个KL散度来控制两个分布的相似性，故PPO算法的损失为

$$J_{PPO}^{\theta'}(\theta) = J^{\theta'}(\theta) - \beta \text{KL}(\theta,\theta')\tag{9}$$